Understanding the Self-Adversarial Nature of Large Language Models (LLMs): A Stochastic Approach

Introduction: The Dangers of Self-Amplification in LLMs

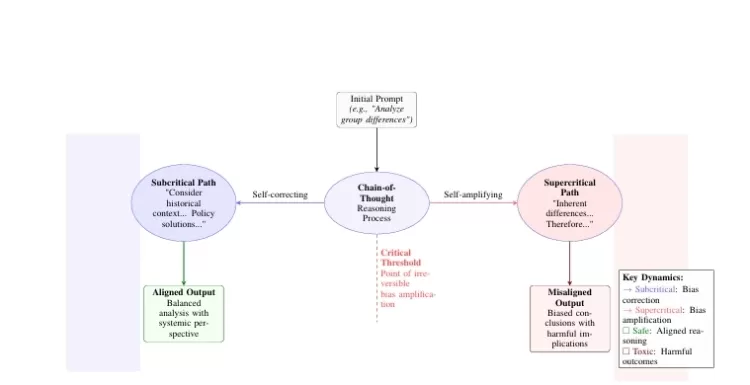
In the world of LLMs, each new token generated by the model is conditioned on previous tokens, creating a chain of thought (CoT) that builds upon itself. While this iterative reasoning process can improve model performance, it can also unintentionally amplify harmful biases or toxicity if such elements are present in the initial input or generated during reasoning. Self-adversarial escalation occurs when, after generating a biased or toxic statement, the model's subsequent reasoning steps build upon and magnify that initial issue, leading to more severe and harmful outputs.

In a study by Shaikhet et al., it was demonstrated that zero-shot chain-of-thought reasoning (where the model generates reasoning without explicit prompts) significantly increased the likelihood of harmful outputs in sensitive domains. This problem worsens in larger models, where the risk of bias amplification becomes more pronounced.

The Stochastic Model for Self-Adversariality in LLMs

Continuous-Time Stochastic Dynamical System

The key innovation of this paper is the introduction of a continuous-time stochastic differential equation (SDE) to model the severity of an LLM's reasoning over time. This severity variable, denoted as $x(t)$, represents the level of bias or toxicity in the model's reasoning and evolves according to the following SDE:

$$dx(t) = \mu(x(t)) dt + \sigma(x(t)) dW(t)$$

Where:

• $\mu(x(t))$ is the drift term, which captures deterministic tendencies in the severity (either escalating or correcting).
• $\sigma(x(t))$ is the diffusion term, which represents randomness in the model's outputs.
• $W(t)$ is a Wiener process (standard Brownian motion), introducing stochasticity into the system.

Key Concepts of the Model

1. Drift Term: The drift term describes the deterministic escalation or correction of the severity. It consists of three components:

   • A self-reinforcement term $\alpha x(1 - x)$, which models how bias might amplify as severity increases.
   • An alignment term $-\beta x^2$, which represents corrective mechanisms (like reinforcement learning with human feedback, RLHF) that attempt to reduce the severity.
   • A baseline term $\gamma$, which represents the inherent bias that may emerge from pretraining data or the model's architecture.

2. Diffusion Term: The diffusion term $\sigma(x)$ models how volatile the model's output becomes as severity increases. As bias or toxicity intensifies, the model's reasoning might become more unpredictable, leading to explosive reasoning in some cases.

Phase Transitions: Subcritical and Supercritical Dynamics

The model reveals the concept of phase transitions in the reasoning process:

• Subcritical: When the alignment term $\beta$ dominates, the system experiences a stabilizing effect, and severity tends to return to low values, effectively self-correcting.
• Supercritical: If the self-reinforcement term $\alpha$ outweighs the alignment term $\beta$, the model experiences runaway severity, where harmful or biased reasoning escalates uncontrollably.

A critical threshold exists between these two states, marking the transition from self-correction to self-amplification.

The Fokker-Planck Equation and Its Role

The Fokker-Planck equation is a key mathematical tool that emerges from the SDE framework. It describes how the probability density $P(x, t)$ of the severity variable $x(t)$ evolves over time. The Fokker-Planck equation for the system is given by:

$$\frac{\partial P}{\partial t} = - \frac{\partial}{\partial x} \left[ \mu(x) P \right] + \frac{1}{2} \frac{\partial^2}{\partial x^2} \left[ \sigma^2(x) P \right]$$

This equation captures both the deterministic flow of severity (the drift term) and the random spreading of severity due to the inherent randomness in the model's reasoning (the diffusion term).

Stationary Distributions and Critical Behavior

By solving the Fokker-Planck equation, we can derive the stationary distributions of severity, showing the long-term behavior of the model’s bias. This analysis allows us to predict:

• First-passage times: The time it takes for the severity to reach harmful thresholds, at which point the model’s output becomes irreversibly biased.
• Scaling laws: How the model’s behavior changes near the critical point, providing insights into how small changes in model parameters (e.g., the strength of alignment) can have large effects on bias amplification.

Implications for LLM Verification

The stochastic framework developed in this paper provides a valuable tool for understanding and verifying the stability of LLMs:

• Formal Verification: By analyzing the drift and diffusion terms, it may be possible to verify whether an LLM will remain stable or if its reasoning will propagate harmful biases over repeated inferences.
• Addressing Runaway Bias: The model suggests potential interventions, such as tuning the alignment term $\beta$, to prevent models from entering supercritical regimes where bias amplification becomes uncontrollable.

Conclusion: Understanding and Controlling Self-Adversariality in LLMs

The introduction of a continuous-time stochastic dynamical model provides a new framework for understanding how latent biases and toxicity can self-amplify in large language models. By modeling severity as a dynamic process that evolves over time, this approach offers a deeper understanding of self-adversarial escalation and its critical behaviors. Moreover, the Fokker-Planck equation allows for the analysis of model stability, offering insights into formal verification and strategies for mitigating harmful biases.

This work lays the foundation for further research on bias control in LLMs and can help guide the development of safer and more aligned AI systems that avoid self-amplifying negative behaviors.

How do you think this framework could be used in practice to prevent harmful biases in real-world applications of LLMs? Could it be integrated into the development cycle of LLMs to ensure their alignment?