This lack of interpretability is particularly problematic in domains where decision-making based on the model’s output can have significant real-world consequences. To address this challenge, the Shapley Value (SV), a concept from cooperative game theory, has emerged as a leading method for explaining the contributions of individual features to a model's output. However, Shapley Values have limitations when it comes to capturing the interactions between multiple features, especially in complex models like GNNs.

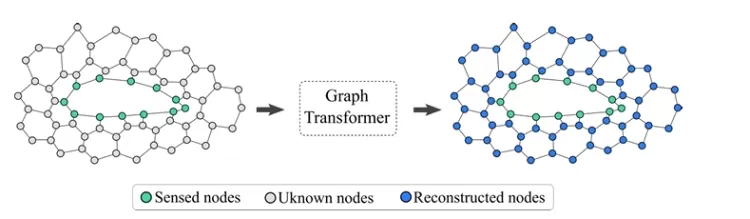
In this work, the authors introduce a novel approach to address the limitations of SVs in explaining GNN predictions by calculating Shapley Interactions (SIs). These interactions extend the concept of SVs to consider joint contributions of multiple features, offering a deeper understanding of how various nodes in a graph contribute to a prediction. The proposed approach, called GraphSHAP-IQ, provides an efficient way to compute any-order Shapley Interactions exactly, overcoming the exponential complexity traditionally associated with these computations.

The Challenge of Interpreting GNN Predictions

GNNs have shown remarkable success in tasks such as graph classification, node classification, and link prediction. However, one of the biggest challenges when using GNNs is their lack of interpretability. Unlike simpler models, such as decision trees, which offer clear explanations of how features contribute to predictions, GNNs involve complex message-passing mechanisms that aggregate information from neighboring nodes in a graph. This architecture makes it difficult to attribute individual predictions to specific features or nodes, especially when there are interactions between different parts of the graph.

To overcome this, Shapley Values were adapted for GNNs to quantify the contribution of individual nodes to a model's prediction. The Shapley Value is a fair method from cooperative game theory that assigns a value to each feature based on its contribution to the final prediction. However, SVs only capture marginal contributions of individual features and fail to account for interactions between features. This is where Shapley Interactions (SIs) come in.

Shapley Interactions: Extending SVs to Interactions Between Nodes

Shapley Interactions extend the concept of Shapley Values by considering joint contributions of multiple features (or nodes, in the case of GNNs) to the final prediction. These interactions are crucial because they help to identify how different parts of the graph work together to influence the model’s output. For example, in a molecular graph, certain atoms may have an independent effect on a molecule's properties, but the interaction between pairs or groups of atoms may also play a critical role. Shapley Interactions enable the quantification of these joint contributions.

However, the computation of Shapley Interactions is computationally expensive. In the case of traditional models, this computation scales exponentially with the number of features, making it impractical for high-dimensional tasks like graph prediction. This is particularly challenging in GNNs, where the number of possible interactions between nodes grows rapidly as the graph size increases.

GraphSHAP-IQ: Efficiently Computing Shapley Interactions

The authors propose GraphSHAP-IQ, a novel method for computing exact Shapley Interactions for GNNs. The key innovation of GraphSHAP-IQ is its ability to leverage the structure of GNNs to reduce the exponential complexity of computing interactions. Instead of requiring an exhaustive search over all subsets of nodes, which is typically required for exact SI computation, GraphSHAP-IQ exploits the receptive fields of the GNN—essentially, the ranges of influence determined by the graph’s connectivity and the number of convolutional layers in the GNN.

By focusing on the receptive fields, GraphSHAP-IQ dramatically reduces the complexity of computing Shapley Interactions. This allows for exact computation of these interactions in a way that is computationally feasible for practical use, even for larger graphs.

Theoretical Contributions:

1. Theoretical Results on GNN Structure: The authors demonstrate that, for graph prediction tasks, the interactions in node embeddings—created through message passing in GNNs—are preserved when transitioning to the final graph prediction. This enables the authors to compute Shapley Interactions in a computationally efficient way by focusing on the receptive fields.
2. Exact Any-Order Interactions: GraphSHAP-IQ is designed to compute Shapley Interactions of any order, including higher-order interactions that involve multiple nodes simultaneously. This provides a more comprehensive explanation of GNN predictions compared to traditional SV-based methods, which only capture single-node contributions.

Practical Contributions:

1. Efficient Calculation: GraphSHAP-IQ significantly reduces the computational cost of calculating exact Shapley Interactions, making it feasible to apply these methods to large real-world datasets.
2. Versatility: The method is applicable to popular GNN architectures and works with standard message-passing techniques, making it a valuable tool for interpreting a wide variety of GNN-based models.
3. Benchmarking: The authors demonstrate the effectiveness of GraphSHAP-IQ on multiple benchmark datasets, showcasing its ability to compute exact Shapley Interactions in practice.

Case Studies:

1. Water Distribution Networks (WDNs): The authors apply GraphSHAP-IQ to interpret predictions made by GNNs on real-world water distribution networks, showing how the method identifies important nodes and their interactions that influence the model’s output.
2. Molecular Graphs: GraphSHAP-IQ is also used to analyze molecule structures, where Shapley Interactions reveal the joint contributions of atoms and substructures to the model’s prediction.

Conclusion

The ability to compute Shapley Interactions exactly is a major advancement in the explainability of Graph Neural Networks. By introducing GraphSHAP-IQ, the authors offer a computationally efficient solution that reduces the complexity of Shapley Interactions from exponential to manageable levels. This makes it feasible to apply exact explanations to real-world graph prediction tasks, improving the interpretability of GNNs.

GraphSHAP-IQ is a promising tool for anyone looking to better understand GNN predictions, whether in scientific domains like molecular chemistry or network analysis, or in broader machine learning applications. The approach not only enables transparency in AI decision-making but also advances the field of explainable AI (XAI) by providing insights into the joint contributions of features in complex graph-structured data.

How do you think the ability to compute Shapley Interactions will change the landscape of GNN interpretability and transparency in machine learning? Let us know your thoughts in the comments below!