Efficient Differentially Private Representations for Set Membership: A New Approach

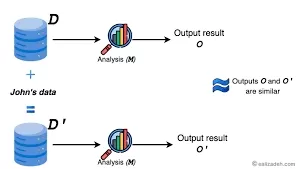
Differential Privacy (DP) is a powerful concept designed to address this challenge. It allows for the sharing of data while safeguarding individual privacy by ensuring that the presence or absence of any single data point does not significantly impact the outcome of an analysis. This paper introduces a groundbreaking solution to the problem of maintaining privacy while sharing set memberships — ensuring that the information does not leak any personal details, even in a large universe of potential data.

The Challenge: Balancing Privacy and Utility

Imagine trying to release a set of websites a user visited from a vast universe of all possible websites. The challenge lies in ensuring that when we release a representation of the set, no individual element in the set is incorrectly flagged as absent (false negative), and no non-member element is falsely added (false positive). This problem becomes more difficult when the universe of possible elements is much larger than the actual set, requiring a compact encoding that still preserves privacy.

Existing techniques like randomized response and Bloom filters provide some level of privacy, but they often suffer from large error rates or inefficient space usage. The question is how to create an encoding that balances privacy guarantees with minimal error and efficient space usage.

Introducing a Novel Approach: Embedding Sets into Random Linear Systems

The authors of this study propose a new way of handling this problem by embedding sets into random linear systems. This method ensures that elements in the set are highly likely to satisfy the corresponding constraints, while elements not in the set are unlikely to do so. This technique, often used in data retrieval systems, is adapted here for the differential privacy setting, resulting in an encoding that is both space-efficient and privacy-preserving.

The paper introduces two primary constructions for different privacy guarantees: approximate differential privacy (ε, δ-DP) and pure differential privacy (ε-DP). Both methods strike an optimal balance between privacy, error rates, and space usage, marking a significant advancement in the field of private data representations.

Key Findings: Optimal Privacy-Utility Trade-offs

The paper presents two key contributions:

1. Approximate-DP Construction: This method achieves an error probability of α = 1 / (e^ε + 1) with a space complexity of 1.05 * k * ε * log(e) bits. The encoding time is proportional to O(k * log(1/δ)), and the decoding time is O(log(1/δ)). This construction ensures efficient space usage while maintaining strong privacy and minimizing error.

2. Pure-DP Construction: A more compact representation with reduced space complexity (k * ε * log(e) bits) but slightly larger decoding times (O(k)). This approach sacrifices some decoding efficiency for better space efficiency.

The optimality of both constructions is confirmed by matching lower bounds on privacy-utility and space-privacy trade-offs, demonstrating that these methods achieve the best possible error probability for any given space and privacy guarantee.

Experimental Evaluation: Proving the Effectiveness

The authors tested their constructions using real-world data and found that their methods produced exponentially smaller error probabilities compared to previous techniques. Moreover, the space usage was optimal, confirming that their approach offers a clear advantage in terms of both privacy and space efficiency.

The experimental results also validate the theoretical analysis, further proving that these methods provide an optimal balance between privacy, utility, and space efficiency.

Exploring the Trade-offs: Privacy, Utility, and Space

The paper delves deeper into the trade-offs between privacy, utility, and space in differential privacy mechanisms. By analyzing the theoretical limits on error probability and space usage, the authors show that their methods achieve the best possible performance in these areas. This rigorous analysis ensures that the proposed constructions are not only effective but also theoretically grounded in the fundamentals of differential privacy.

Related Work: Overcoming the Limitations of Previous Methods

Previous research on private set representations has often relied on methods like Bloom filters, which inject noise into the set representations to achieve privacy. While these techniques offer some degree of protection, they suffer from high error probabilities and inefficient space usage. In contrast, the authors' novel approach of embedding sets into random linear systems provides both lower error rates and more efficient space usage, making it a significant improvement over previous methods.

Conclusion: A Major Leap Forward in Private Set Representations

This paper introduces two efficient algorithms for constructing differentially private representations of sets, achieving optimal privacy-utility and space-privacy trade-offs. By embedding sets into random linear systems, the authors overcome the shortcomings of previous methods that relied on noise injection. The experimental results further confirm the superiority of these methods, making them a promising solution for privacy-preserving data analytics.

As privacy concerns continue to grow, these methods could play a pivotal role in scenarios like web traffic analysis or personal data sharing, where the need to protect individual privacy without sacrificing analytical utility is critical.

Looking Ahead: Applying Differential Privacy to Real-World Challenges

As we move toward an era where data sharing and analysis are increasingly common, these advances in differentially private set representations offer a powerful tool for protecting privacy. The real-world applications are vast, from ensuring the privacy of user activity data for web traffic analysis to enabling the safe sharing of personal information for research purposes. The challenge lies in extending these methods to handle more complex data structures and multi-set representations.

In the context of real-world privacy challenges, how do you think these advances could be applied to fields like healthcare data analysis or personalized advertising? Feel free to share your thoughts below!