Temporally Adaptive Interpolated Distillation (TAID): Overcoming Teacher-Student Disparities for Efficient Model Compression

making it difficult to deploy them efficiently, especially on resource-constrained devices like smartphones and edge devices. This scaling paradox limits the accessibility of cutting-edge AI technologies, preventing them from reaching their full potential in real-world applications.

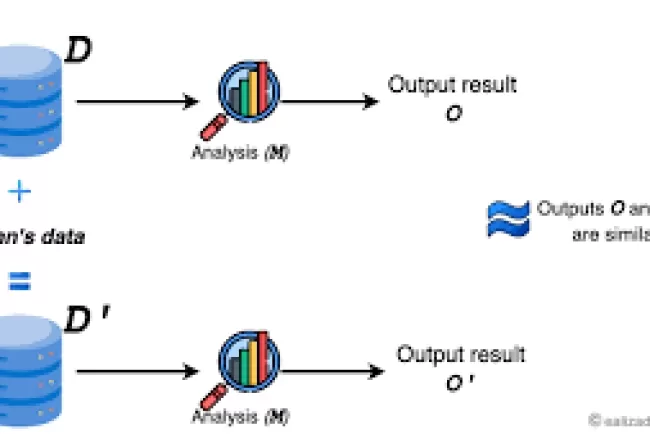
Knowledge distillation (KD) has emerged as a promising solution to this problem by enabling the transfer of knowledge from a large, powerful "teacher" model to a smaller, more efficient "student" model. While traditional KD techniques have made strides in improving model efficiency, challenges such as capacity gaps between teacher and student models, as well as issues like mode averaging and mode collapse, persist. In response to these challenges, the authors introduce Temporally Adaptive Interpolated Distillation (TAID)—a novel approach designed to improve knowledge transfer during distillation, making compact models more effective without compromising performance.

Understanding the Core Concepts:

• Knowledge Distillation (KD): KD is a technique where knowledge from a larger, well-trained model (the teacher) is transferred to a smaller model (the student) to create a more efficient version. The goal is to maintain the performance of the larger model while making it suitable for environments with limited resources.

• Capacity Gap: The difference in size and complexity between the teacher and student models. A large teacher model contains much more detailed knowledge, but the student model may not have the capacity to absorb all of that information, resulting in suboptimal performance.

• Mode Averaging and Mode Collapse: These are common issues in knowledge distillation. Mode averaging happens when the student model becomes too generalized, losing the richness of the teacher’s distribution. Mode collapse occurs when the student model focuses too heavily on a few specific aspects of the teacher's output, ignoring other important information.

The TAID Approach: A Dynamic Solution to Model Disparities

TAID introduces a solution to these distillation challenges by using adaptive intermediate teacher distributions. The core concept behind TAID is to allow the student model to gradually shift from its own distribution towards the teacher's distribution, adapting as training progresses. This gradual interpolation helps mitigate the impact of the capacity gap and prevents mode averaging and mode collapse.

How TAID Works:

• Capacity Gap: By interpolating between the distributions of the teacher and the student, TAID reduces the impact of the teacher's large capacity. The student model can absorb knowledge in a way that matches its smaller size, leading to a more efficient learning process.

• Mode Averaging: TAID’s time-dependent interpolation ensures that the student model doesn’t lose the richness of the teacher’s knowledge. Rather than overwhelming the student with the teacher's complexity too early, TAID allows for a gradual integration of the teacher's knowledge.

• Mode Collapse: The dynamic interpolation prevents the student model from focusing on just a few dominant aspects of the teacher's knowledge. Instead, the student begins by learning from its own distribution, slowly adapting to incorporate the teacher's more nuanced knowledge as training progresses.

Theoretical Foundation of TAID

TAID’s interpolation mechanism is grounded in a theoretical framework that utilizes Kullback-Leibler (KL) divergence to measure the difference between the intermediate teacher-student distribution and the student model's predictions. By minimizing this divergence, the model is guided to approximate the teacher’s outputs without overwhelming its capacity.

The adaptive interpolation parameter (