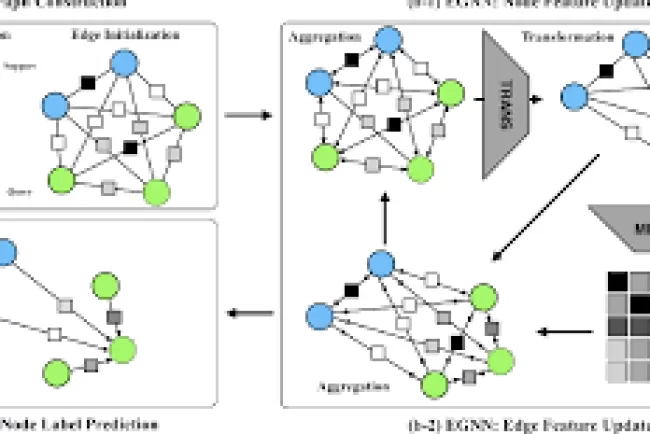
Modus Ponens and Modus Tollens

Modus Ponens and Modus Tollens are two fundamental rules of inference in propositional logic. They allow us to derive conclusions from given premises using valid logical reasoning. However, incorrect applications can lead to logical fallacies, such as assuming the inverse or assuming the converse.

Computer Science Feb 1, 2025 0 11 Add to Reading List

1. Modus Ponens

Definition:

Modus Ponens (Latin for "mode that affirms") is a valid rule of inference that allows us to conclude the consequent when both the conditional statement and its antecedent are true.

Logical Form:

$(P \rightarrow Q), \quad P \quad \therefore Q$

Where:

$P$ = Antecedent ("if" part of the statement)
$Q$ = Consequent ("then" part of the statement)
$P \rightarrow Q$ = Conditional statement ("If P, then Q")

Example:

Premise 1: If it rains ( $P$ ), then the ground will be wet ( $Q$ ).
Premise 2: It is raining ( $P$ ).
Conclusion: Therefore, the ground is wet ( $Q$ ). ✅

Truth Table for Modus Ponens:

$P$	$Q$	$P \rightarrow Q$	$P$	Conclusion ( $Q$ )
T	T	T	T	T
T	F	F	T	F
F	T	T	F	?
F	F	T	F	?

Note: The question marks indicate cases where Modus Ponens cannot be applied, meaning the premises do not lead to a necessary conclusion.

2. Modus Tollens

Definition:

Modus Tollens (Latin for "mode that denies") is a valid rule of inference that allows us to deny the antecedent when both the conditional statement and the negation of the consequent are true.

Logical Form:

$(P \rightarrow Q), \quad \neg Q \quad \therefore \neg P$

Where:

$P$ = Antecedent ("if" part of the statement)
$Q$ = Consequent ("then" part of the statement)
$\neg Q$ = The consequent is false
$\neg P$ = Conclusion: the antecedent must also be false

Example:

Premise 1: If it is raining ( $P$ ), then the ground will be wet ( $Q$ ).
Premise 2: The ground is not wet ( $\neg Q$ ).
Conclusion: Therefore, it is not raining ( $\neg P$ ). ✅

Truth Table for Modus Tollens:

$P$	$Q$	$P \rightarrow Q$	$\neg Q$	Conclusion ( $\neg P$ )
T	T	T	F	?
T	F	F	T	F
F	T	T	F	?
F	F	T	T	T

Note: The question marks indicate cases where Modus Tollens cannot be applied, meaning the premises do not lead to a necessary conclusion.

Logical Fallacies Related to Modus Ponens and Modus Tollens

Fallacy 1: Assuming the Converse (Invalid Reasoning)

Incorrect Assumption: $(P \rightarrow Q)$ means that $(Q \rightarrow P)$ is also true.
Logical Form (Fallacy): $(P \rightarrow Q), Q \quad \therefore P$
Example:
1. If it rains ( $P$ ), then the ground is wet ( $Q$ ).
2. The ground is wet ( $Q$ ).
3. Incorrect Conclusion: Therefore, it is raining ( $P$ ). ❌ (Wrong Reasoning)
- Why is this wrong? The ground could be wet for other reasons (e.g., a sprinkler).

Fallacy 2: Assuming the Inverse (Invalid Reasoning)

Incorrect Assumption: $(P \rightarrow Q)$ means that $(\neg P \rightarrow \neg Q)$ is also true.
Logical Form (Fallacy): $(P \rightarrow Q), \neg P \quad \therefore \neg Q$
Example:
1. If it rains ( $P$ ), then the ground is wet ( $Q$ ).
2. It is not raining ( $\neg P$ ).
3. Incorrect Conclusion: Therefore, the ground is not wet ( $\neg Q$ ). ❌ (Wrong Reasoning)
- Why is this wrong? The ground could still be wet due to other causes (e.g., someone watering the garden).

Summary Table of Valid and Invalid Inferences

Rule/Fallacy	Logical Form	Valid?
Modus Ponens	$(P \rightarrow Q), P \Rightarrow Q$	✅ Yes
Modus Tollens	$(P \rightarrow Q), \neg Q \Rightarrow \neg P$	✅ Yes
Fallacy of Assuming the Converse	$(P \rightarrow Q), Q \Rightarrow P$	❌ No
Fallacy of Assuming the Inverse	$(P \rightarrow Q), \neg P \Rightarrow \neg Q$	❌ No

Conclusion

Modus Ponens and Modus Tollens are valid rules of inference, ensuring logical consistency in reasoning.
Fallacies arise when people mistakenly assume the inverse or converse of a conditional statement is valid.
These concepts are widely used in mathematics, science, AI, philosophy, and legal reasoning.