Quantum computing is undergoing a transformative phase with the emergence of logical quantum processors, which hold the potential to solve complex problems that classical computers cannot efficiently address. However, despite significant progress, applying quantum algorithms to real-world problems remains a daunting challenge. One area of focus is hybrid quantum-classical methods, which aim to harness the strengths of both quantum and classical systems to solve problems in a more scalable and efficient manner.

In this blog, we explore a novel approach known as the Conditional Generative Quantum Eigensolver (conditional-GQE), which uses a quantum-classical hybrid model for combinatorial optimization. This new methodology significantly advances quantum circuit generation, offering insights into how quantum systems can be applied to complex real-world tasks. Let’s dive into the workings of generative quantum combinatorial optimization (GQCO), its potential applications, and the breakthroughs it brings to the world of quantum computing.

What is Conditional-GQE?

Generative Quantum Eigensolver (GQE) is a hybrid quantum-classical algorithm designed to generate quantum circuits by leveraging classical machine learning models. It combines the power of classical generative models with quantum circuits to solve complex optimization problems, such as combinatorial optimization. Traditionally, quantum circuits are designed by embedding classical information (like data) into the circuit, which can limit the expressibility of the quantum system. The key breakthrough with GQE is its ability to generate quantum circuits without embedding classical parameters directly into the quantum circuit.

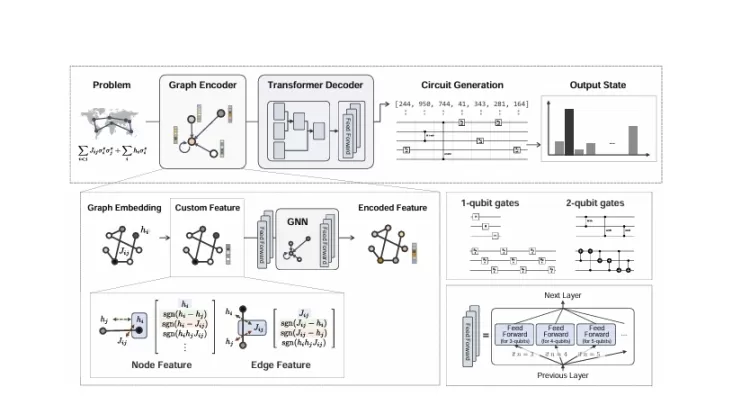
However, previous versions of GQE, such as GPT-QE, struggled with generalizing across different problem contexts because they didn’t incorporate contextual inputs into the generative model. To overcome this limitation, conditional-GQE introduces context-aware quantum circuit generation by employing an encoder-decoder Transformer architecture. This structure allows the model to generate quantum circuits that are tailored to solve specific problems by processing input data more flexibly and efficiently.

How Does Conditional-GQE Work?

The main idea behind conditional-GQE is to create a quantum circuit generation process that is dependent on the context or the problem at hand. Instead of re-training the model every time a new problem is encountered, the trained model can be adapted to any context without needing retraining, thus improving scalability.

The process involves the following steps:

1. Input Context: The problem context is encoded into the model using an encoder-decoder Transformer architecture. For combinatorial optimization, this context is typically represented as a graph derived from the Ising model, which is commonly used for optimization problems.
2. Quantum Circuit Generation: The encoded features are then passed through the decoder, which generates quantum gates that are sequenced together to form a complete quantum circuit. The circuit is designed to minimize the energy (observable) of the system, thereby finding an optimal solution to the problem.
3. Optimization: Using preference-based training, the quantum circuit is iteratively optimized, with the model adjusting its parameters based on feedback from the measurements of the quantum state after running the circuit.

This architecture not only allows for efficient quantum circuit generation but also introduces a new way to incorporate graph neural networks (GNNs) into the circuit design, making the process even more adaptable and accurate for solving complex optimization tasks.

Key Contributions and Findings

1. Scalability and Generalization

One of the main advantages of conditional-GQE is its ability to handle combinatorial optimization problems with up to 10 qubits efficiently. The model has shown a 99% accuracy rate in solving new test problems, outperforming traditional methods such as brute-force approaches, simulated annealing (SA), and even the quantum approximate optimization algorithm (QAOA).

2. Preference-Based Optimization (DPO)

Conditional-GQE introduces a dataset-free, preference-based optimization method that significantly reduces computational overhead. Unlike traditional supervised or reinforcement learning methods, which rely on labeled data or intermediate quantum states, the Direct Preference Optimization (DPO) strategy directly optimizes quantum circuits by comparing the final measurement results of the generated circuits. This novel approach avoids the need for costly simulations of quantum states and enables large-scale quantum systems to be handled more efficiently.

3. Quantum-Classical Hybrid Approach

By integrating classical and quantum systems, conditional-GQE combines the flexibility and expressiveness of classical generative models with the computational power of quantum circuits. This hybrid approach enhances the performance of quantum algorithms while addressing the limitations of current quantum devices, which often suffer from noise and limited qubit connectivity.

4. Mixture-of-Experts (MoE) Architecture

The conditional-GQE framework utilizes a Mixture-of-Experts (MoE) architecture to increase the expressiveness of the model. This allows the system to handle a wider range of optimization problems by enabling the quantum circuit to adaptively choose between different components based on the problem context, leading to more efficient solutions.

Applications of Generative Quantum Combinatorial Optimization

Combinatorial optimization problems are pervasive in various fields, including logistics, finance, and machine learning. Solving these problems efficiently can lead to significant advancements in industries like:

• Supply Chain Management: Optimizing routes, inventories, and resource allocations.
• Machine Learning: Enhancing optimization in hyperparameter tuning and neural network training.
• Quantum Chemistry: Accelerating drug discovery and material design by solving optimization problems related to molecular structures.

The GQCO framework can provide a powerful tool for tackling these problems, especially in cases where classical optimization methods are inefficient or unable to scale.

Challenges and Future Directions

While the progress shown by conditional-GQE is promising, there are still challenges to address:

• Noise and Imperfect Quantum Devices: As quantum hardware matures, minimizing noise and improving qubit connectivity will be crucial for maximizing the effectiveness of quantum algorithms.
• Scalability to Larger Problems: While the model performs well for problems with up to 10 qubits, scaling to larger systems will require further optimizations in circuit design and training techniques.

Future research will focus on refining the preference-based optimization methods and expanding the range of applications to more complex problems. Moreover, researchers are exploring ways to improve quantum error correction to enhance the robustness of quantum circuits for real-world applications.

Conclusion

The introduction of conditional-GQE marks a significant step forward in quantum circuit generation, enabling the efficient solution of combinatorial optimization problems through a hybrid quantum-classical approach. By incorporating context-aware generation and leveraging advanced techniques such as preference-based training and graph neural networks, this approach opens new possibilities for solving complex real-world problems. As quantum devices continue to evolve, the integration of such innovative techniques will play a crucial role in accelerating the adoption of quantum computing across various domains.

Stay tuned for more advancements in quantum combinatorial optimization and the future of hybrid quantum-classical algorithms! What are your thoughts on the potential of quantum circuit generation for solving optimization problems? Share your insights in the comments below!