The Challenge: Robust Reasoning in LLMs

Despite the incredible advancements made in LLMs, there are still significant hurdles when it comes to logical reasoning. These models, while capable of reasoning through simple tasks, struggle when faced with more complex problems that require precise logical formulation. This issue is exacerbated when reasoning tasks involve multiple steps or ambiguous problem definitions, as LLMs tend to make errors that affect the final solution.

One prominent strategy to improve LLM reasoning is Chain-of-Thought (CoT) prompting, where the model is asked to articulate intermediate steps before deriving the final answer. While CoT has led to some improvements, challenges like logical inconsistencies persist, especially when the tasks are complex. This has led researchers to explore combining LLMs with logical solvers, where LLMs help formalize a problem, and the solver guarantees logical consistency.

However, the combination of LLMs and solvers has its own set of issues. For example, generating a correct formal representation of a problem from natural language is tricky and error-prone. Even when automated reasoning tools are employed, their accuracy often remains insufficient, leaving the burden of manual verification on users, which is not feasible for more intricate problems.

Introducing Semantic Self-Verification (SSV)

The Semantic Self-Verification (SSV) approach proposed by MohammadRaza and Natasa Milic-Frayling offers a reliable and effective method to address these challenges. It focuses on improving the accuracy of reasoning by verifying that the formalization of a problem generated by an LLM matches the original intent. This approach not only increases reasoning accuracy but also reduces the need for manual verification.

Key Features of SSV:

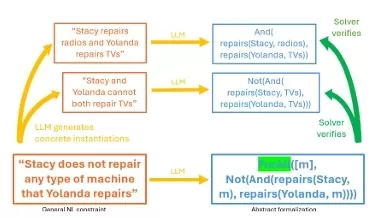
1. Consistency-Based Verification: The core idea behind SSV is to verify that the abstract formalization of a problem is consistent with concrete examples or instantiations. Instead of only relying on a single abstract translation, the system also generates concrete instances of the problem, which are used to verify that the formalization satisfies the intended constraints.

2. Near-Certain Confidence: SSV goes beyond traditional approaches by introducing a verification mechanism that provides near-certain confidence in the correctness of the reasoning process. This is akin to a consensus-based ensemble where different tasks are tackled by independent predictors (such as generating abstract and concrete inferences), and the logical solver checks the consistency of these results.

3. Dynamic Error Refinement: One of the novel aspects of SSV is that any failure in verification can guide improvements in the formalization process. By identifying where and why a formalization fails, the system can automatically refine its reasoning model to handle similar problems more effectively in the future.

How Does SSV Work?

Let’s break down the process of Semantic Self-Verification:

1. Formulation: The model first translates the problem from natural language (e.g., a legal reasoning task or a mathematical puzzle) into a formal language that can be processed by a solver.

2. Concrete Instantiations: The model then generates several concrete instances of the problem to test whether the formal representation holds true in various scenarios. These instantiations are diverse examples drawn from the problem's constraints and conditions.

3. Verification: Each of these concrete instances is validated using a logical solver (e.g., Z3 solver, a state-of-the-art tool for verifying logical expressions). If the solver verifies that the formal representation satisfies the instances, the solution is considered verified.

4. Confidence Scoring: Finally, the system produces an answer with a confidence score indicating whether it is confident in the solution's correctness. If verification passes, the system can claim near-perfect certainty.

Example: The Law School Admissions Test (LSAT) Problem

Consider the example provided from the Law School Admissions Test (LSAT) for analytical reasoning:

Problem: There are six technicians (Stacy, Urma, Wim, Xena, Yolanda, and Zane), each repairing different types of machines. Various conditions dictate who repairs what. The task is to determine which pair of technicians repairs the same types of machines.

Formalization: SSV helps in converting this problem into a formal constraint representation, which the solver can then verify. By generating concrete instantiations of the technician-machine assignment and testing each possibility, the solver can accurately verify the correct answer, which would be "Urma & Xena" (Option C), ensuring that their formalization is correct.

Empirical Results

The results of using SSV on challenging reasoning tasks, such as the AR-LSAT dataset, have been promising. SSV demonstrated:

• Significantly improved accuracy compared to traditional LLM-based inference and Chain-of-Thought methods.
• Near-perfect precision in verified cases, meaning the model can confidently offer correct answers with minimal need for human oversight.
• Robust performance on a wide range of reasoning tasks, showing that the approach can handle both simple and complex problems.

Benefits of SSV

• Reduces Human Error: By providing a high-confidence verification mechanism, SSV reduces the need for manual verification, which is especially important for complex tasks.
• Improves Model Reliability: The consistency-based approach ensures that models are more reliable, offering greater assurance in the correctness of the output.
• Scalable for Complex Reasoning: SSV can be applied to increasingly complex problems, making it a scalable solution for AI-driven reasoning tasks across domains like law, medicine, and mathematics.

Conclusion

Semantic Self-Verification is a groundbreaking approach to improving the robustness and reliability of logical reasoning in AI systems. By ensuring that reasoning formalizations are consistent with concrete examples and verified by logical solvers, SSV makes AI-driven reasoning more dependable. This approach could play a crucial role in reducing human error and making AI systems more reliable for real-world applications, moving us closer to achieving dependable and autonomous AI reasoning systems.

How do you think SSV could be applied to other domains, such as legal or medical reasoning? Let us know your thoughts in the comments below!